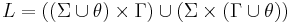Morphological dictionary
In the field of computational linguistics, a morphological dictionary is a linguistic resource that contains correspondences between surface form and lexical forms of words. Surface forms of words are those found in any text. The corresponding lexical form of a surface form is the lemma followed by grammatical information (for example the part of speech, gender and number). In English houses is a surface form of the noun house. The lexical form would be "house", noun, plural. There are two kinds of morphological dictionaries: aligned and non-aligned.
Contents |
Aligned morphological dictionaries
In an aligned morphological dictionary, the correspondence between the surface form and the lexical form of a word is aligned at the character level. Continuing with the previous example, we have:
- (h,h) (o,o) (u,u) (s,s) (e,e) (s,<n>), (θ,<pl>)
Where θ is the empty symbol and <n> signifies "noun", and <pl> signifies "plural".
In the example the left hand side is the surface form (input), and the right hand side is the lexical form (output). This order is used in morphological analysis where a lexical form is generated from a surface form. In morphological generation this order would be reversed.
Formally, if Σ is the alphabet of the input symbols, and  is the alphabet of the output symbols, an aligned morphological dictionary is a subset
is the alphabet of the output symbols, an aligned morphological dictionary is a subset 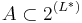 , where:
, where:
is the alphabet of all the possible alignments including the empty symbol. That is, an aligned morphological dictionary is a set of string in 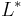 .
.
Non-aligned morphological dictionary
A non-aligned morphological dictionary is simply a set 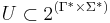 of pairs of input and output strings. A non-aligned morphological dictionary would represent the previous example as:
of pairs of input and output strings. A non-aligned morphological dictionary would represent the previous example as:
- (houses, house<n><pl>)
It is possible to convert a non-aligned dictionary into an aligned dictionary. Besides trivial alignments to the left or to the right, linguistically motivated alignments which align characters to their corresponding morphemes are possible.
Lexical ambiguities
Frequently there exists more than one lexical form associated with a surface form of a word. For example "house" may be a noun in the singular, /haʊs/, or may be a verb in the present tense, /haʊz/. As a result of this it is necessary to have a function which relates input strings with their corresponding output strings.
If we define the set 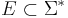 of input words such that
of input words such that 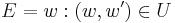 , the correspondence funcion would be
, the correspondence funcion would be 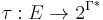 defined as
defined as 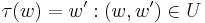 .
.
List of online morphological dictionaries
- Canoo.net – German
- Babelpoint.org – English
- Babelpoint.org – French
- Babelpoint.org – German
- Babelpoint.org – Russian
- Babelpoint.org – Spanish
- Babelpoint.org – Swedish
References
- Garrido-Alenda, A. and Forcada, M. L. (2002). "Comparing nondeterministic and quasideterministic finite-state transducers built from morphological dictionaries". Procesamiento del Lenguaje Natural, (XVIII Congreso de la Sociedad Española de Procesamiento del Lenguaje Natural, Valladolid, Spain, 11-13.09.2002)